modèle auto-regressif du second ordre

À partir de maintenant, nous reprendrons la notation de Purser et McQuigg (1982) [12] , Hayden et Purser (1995) [7], Purser et al (2002) [13] et Lorenc (1992) [10] :

$$\left\{ \begin{array}{ll} q_{i}=(1-\alpha)p_{i} + \alpha q_{i-1} & \... ...\alpha)q_{i} + \alpha s_{i+1} & \textrm{pour $i=n,\cdots,1$} \end{array}\right.$$ (A.13)

Où $p_i$ est la valeur initiale au point de grille $i$, $q_i$ est la valeur après le filtrage de $i=1$ à $n$, $s_i$ est la valeur après le passage du filtre dans chaque direction et $\alpha$ est le coefficient de filtrage.

Ceci est donc un filtre recursif du premier ordre qui doit être appliqué dans les deux directions pour assurer que la phase reste nulle.

Des filtres d'ordre supérieur peuvent être fabriqués en appliquant plusieurs fois le filtre de premier ordre (A.13). Dans ce cas, les conditions limites changent après chaque application du filtre. L'étude des conditions limites sera effectuée dans la section A.3. Cependant, au premier ordre, et comme étudié dans la section A.1, les conditions limites en $i=1$ et $i=n$, sont :

$$\left\{ \begin{array}{ll} q_{1}=(1-\alpha)p_1\\ s_n=\frac{1}{1+\alpha}q_n \end{array}\right.$$ (A.14)

À la différence de la section A.1, les conditions limites sont données à l'intérieur du domaine et non à l'extérieur.

Pour analyser plus facilement le filtre, il est intéressant de considérer son inverse, qui n'est pas récursif. Après réarrangement de (A.13), on trouve :

$$p_i = s_i - \frac{\alpha}{(1-\alpha)^2}(s_{i-1}-2s_i+s_{i+1})$$ (A.15)

Si on calcule le réponse spectrale du filtre récursif, il faut définir $s$ tel que $s = \sum s_i \delta_{t_i}$ avec $\delta_{t_i}$ le dirac au temps $t_i$, alors :

$$\mathfrak{F}(p_i) = \int p_i \delta_{t_i} e^{-ikt} dt$$

$$= \int s_i \delta_{t_i} e^{-ikt} dt$$

$$- \frac{\alpha}{(1-\alpha)^2} \Bigg( \int s_{i-1} \delta_{t_{i-1}} ... ...s_i \delta_{t_i} e^{-ikt} dt + \int s_{i+1} \delta_{t_{i+1}} e^{-ikt} dt \Bigg)$$ (A.16)

En définissant $s_i$ comme une onde telle que $s_i = e^{ikt_i}$, on trouve alors :

$$\mathfrak{F}(p_i) = \int e^{ikt_i} \delta_{t_i} e^{-ikt} dt$$

$$- \frac{\alpha}{(1-\alpha)^2} \Bigg( \int e^{ikt_{i-1}} \delta_{t_{... ...elta_{t_i} e^{-ikt} dt + \int e^{ikt_{i+1}} \delta_{t_{i+1}} e^{-ikt} dt \Bigg)$$

$$= \int \delta_{t_i} dt - \frac{\alpha}{(1-\alpha)^2} \Bigg( \int e^... ...int \delta_{t_i} dt + \int e^{ik(t_i+\delta t)} \delta_{t_i} e^{-ikt} dt \Bigg)$$

$$= \int \delta_{t_i} dt - \frac{\alpha}{(1-\alpha)^2} \Bigg( \int e^... ..._{t_i} dt - 2 \int \delta_{t_i} dt + \int e^{ik\delta t} \delta_{t_i} dt \Bigg)$$

$$= 1 - \frac{\alpha}{(1-\alpha)^2} \Bigg( e^{ik\delta t} - 2 + e^{ik\delta t} \Bigg)$$

$$= 1 - \frac{\alpha}{(1-\alpha)^2} \Bigg( 2\cos(k\delta t) - 2 \Bigg)$$

$$= 1 - \frac{2\alpha}{(1-\alpha)^2} \Bigg( \bigg( 1 - 2\sin^2(\frac{k\delta t}{2}) \bigg) - 1 \Bigg)$$

$$= 1 + \frac{\alpha}{(1-\alpha)^2} \Bigg( 2\sin(\frac{k\delta t}{2}) \Bigg)^2$$

La réponse spectrale de l'inverse du filtre est alors :

$$S_{1pass}(k) = \frac{1}{1+\frac{\alpha}{(1-\alpha)^2}\Big(2\sin(\frac{k\delta t}{2})\Big)^2}$$ (A.17)

Et pour un filtre d'ordre $N$, ce facteur doit être appliqué $N$ fois. Si $k\delta t$ et $\alpha$ sont petits, alors en appliquant les développement de Taylor à l'ordre un, on trouve :

$$S_{Npass}(k) \simeq 1-\frac{\alpha}{(1-\alpha)^2}Nk^2\delta t^2$$ (A.18)

Ce filtre doit alors être comparé à l'effet de la convolution d'un champs par une fonction de covariance. Dans notre cas, nous voulons utiliser une fonction auto-regressive du second ordre (SOAR) car elle est plus énergétique que la classique fonction de covariance de Gauss.

$$b(t) = \varepsilon_b^2 \bigg( 1 + \frac{\vert t\vert}{\tau}\bigg) e^{-\frac{\vert t\vert}{\tau}}$$ (A.19)

Il faut alors calculer la transformée de Fourier de la fonction SOAR :

$$S_{SOAR}(k) = \mathfrak{F}(b(t)) = \varepsilon^2 \int_{-\infty}^{+\infty} b(x) e^{-ikt} dt$$

$$= \varepsilon^2 \int_{-\infty}^{+\infty} \Big( e^{-\frac{\vert t\ve... ...- ikt} + \frac{\vert t\vert}{\tau} e^{-\frac{\vert t\vert}{\tau} - ikt}\Big) dt$$

$$= \varepsilon^2 \Bigg[ \int_{-\infty}^0 e^{\frac{t}{\tau}-ikt}dt + ... ...} - ikt}dt + \int_0^{+\infty} \frac{t}{\tau} e^{-\frac{t}{\tau} - ikt}dt \Bigg]$$

$$= \varepsilon^2 \Bigg[ \int_0^{+\infty} \Big( e^{-\frac{t}{\tau}-ik... ...^{-\frac{t}{\tau}-ikt} + \frac{t}{\tau} e^{-\frac{t}{\tau}+ikt} \Big) dt \Bigg]$$

$$= \varepsilon^2 \Bigg[ \int_0^{+\infty} \Big( e^{-t(\frac{1}{\tau}+... ...\Big( t e^{-t(\frac{1}{\tau}+ik)} + t e^{-t(\frac{1}{\tau}-ik)} \Big) dt \Bigg]$$ (A.20)

On reconnait les intégrales de la forme $\int_0^{+\infty}x^n e^{-ax} dx = \frac{\Gamma(n+1)}{a^{n+1}}$. L'équation A.21 peut alors se résoudre :

$$S_{SOAR}(k) = \varepsilon^2 \bigg[ \frac{\tau}{1+i\tau k} + \frac{\tau}{1-i\tau k} + \frac{\tau}{(1+i\tau k)^2} + \frac{\tau}{(1-i\tau k)^2} \bigg]$$

$$= \tau \varepsilon^2 \bigg[ \frac{2}{1+\tau^2 k^2} + \frac{2 - 2\tau^2k^2}{(1+\tau^2 k^2)^2} \bigg]$$

$$= \varepsilon_b^2 \frac{4\tau}{(1+k^2\tau^2)^2}$$ (A.21)

En appliquant les développement de Taylor à l'ordre un, on obtient alors :

$$S_{SOAR}(k) \simeq \varepsilon_b^2 4\tau (1-2k^2\tau^2)$$ (A.22)

En supposant que $k\delta t$ est petit, il est possible d'obtenir une fonction SOAR avec le filtre récursif, car (A.23) est similaire à (A.19) pour $N=2$.

Il est alors possible de définir un facteur d'échelle $\beta$ tel que :

$$\beta = \varepsilon_b^2 4\tau$$ (A.23)

Il faut alors définir $\alpha$ tel que :

$$\frac{\alpha}{(1-\alpha)^2}Nk^2\delta t^2 = 2k^2\tau^2$$ (A.24)

En posant $E=\frac{N\delta t^2}{4\tau}$, on obtient le polynôme du deuxième ordre :

$$\alpha^2 -2(1+E)\alpha+1 = 0$$ (A.25)

En le résolvant, on trouve $\alpha$ :

$$\alpha = 1 + E - \sqrt{E(E+2)}$$ (A.26)

Si on calcule la l'échelle de corrélation du filtre récursif en appliquant la formule 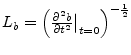$L_b = \Big( \frac{\partial^2 b}{\partial t^2}\big\vert _{t=0} \Big)^{-\frac{1}{2}}$, on trouve que $L_b = \tau$.

Comme $N$ est fixé à 2 et que $\delta t$ est fixé par la grille, il apparaît que $\alpha$ ne dépend que de l'échelle de corrélation $\tau$.