À chaque itération de la minimisation, le terme de la fonction coût lié
aux observations
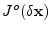 est calculé en propageant l'incrément
est calculé en propageant l'incrément
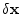 dans le temps avec le modèle linéaire-tangent
dans le temps avec le modèle linéaire-tangent 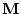 .
Le calcul du gradient de la fonction coût, notamment de la partie relative
aux observations
.
Le calcul du gradient de la fonction coût, notamment de la partie relative
aux observations
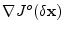 , nécessite l'intégration
de l'adjoint du modèle linéaire-tangent
, nécessite l'intégration
de l'adjoint du modèle linéaire-tangent 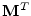 sur la fenêtre d'assimilation.
À la fin de la minimisation, l'incrément d'analyse est ajouté à l'ébauche
sur la fenêtre d'assimilation.
À la fin de la minimisation, l'incrément d'analyse est ajouté à l'ébauche 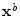 (Eq. 5.35). L'état analysé à l'instant initial de la fenêtre
d'assimilation
(Eq. 5.35). L'état analysé à l'instant initial de la fenêtre
d'assimilation 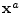 est ensuite propagé par le modèle non-linéaire
est ensuite propagé par le modèle non-linéaire 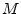 jusqu'à la fin
de la fenêtre permettant d'obtenir une trajectoire analysée
jusqu'à la fin
de la fenêtre permettant d'obtenir une trajectoire analysée
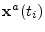 .
En pratique, il est possible de prendre en compte les faibles non-linéarités
des opérateurs
.
En pratique, il est possible de prendre en compte les faibles non-linéarités
des opérateurs 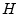 et
et 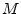 en mettant à jour la trajectoire de référence au cours de
la minimisation. Ces mises à jours sont aussi appelée boucles externes.
Le modèle linéaire est relinéarisé au voisinage du nouvel état de référence à chaque
boucle externe et la fonction coût est ensuite minimisée par une série de boucles
internes. Cette méthode permet de conserver la fonction coût quadratique tout en
tenant compte, jusqu'à un certain point, des non-linéarités du système.
en mettant à jour la trajectoire de référence au cours de
la minimisation. Ces mises à jours sont aussi appelée boucles externes.
Le modèle linéaire est relinéarisé au voisinage du nouvel état de référence à chaque
boucle externe et la fonction coût est ensuite minimisée par une série de boucles
internes. Cette méthode permet de conserver la fonction coût quadratique tout en
tenant compte, jusqu'à un certain point, des non-linéarités du système.
Nicolas Daget
2007-11-16