Unwrap a blade’s skin

Description

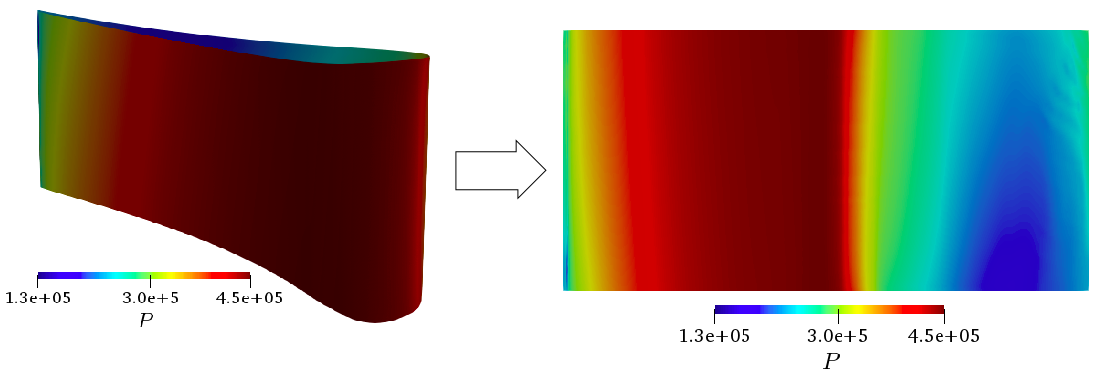
Unwrap a 3D blade into a 2D plan.

image

Warning

dependency on:

Parameters

  • base: Base

    The input base must correspond to the blade’s skin. In addition, the variable CoordinateReducedHeight computed from the antares.treatment.turbomachine.TreatmenthH must be included in the input base.

  • variables: list(str), default = None

    Names of variables present in the input base that will also be in the output base. If None, all input variables will be conserved. Variables like ‘d’, ‘d_D’ and ‘R’ respectively associated to curvilinear coordinate and its reduced form, and the radius.

  • number_of_heights: int, default = 101

    The number of iso-h/H needed to discretize the blade through the variable CoordinateReducedHeight.

  • number_of_d_D: int, default = 1001

    The number of discretization along the blade’s curvilinear coordinate. This number has to be strictly greater than one.

  • begin_unwrap: str, default = ‘LE’

    Convention : ‘LE’ (leading edge) or ‘TE’ (trailing edge). In other words, either sort the blade from the LE to the TE or vice versa. Therefore, if begin_unwrap is set to ‘LE’, the curvilinear coordinate’s zero is at the leading edge.

  • p_var: str, default = ‘Psta’

    Name of the pressure variable. Necessary to discriminate pressure from suction side on every profile.

  • h_H_name: str, default = ‘CoordinateReducedHeight’

    Name of the coordinate reduced height variable.

  • h_H_range: str, default = None

    Either None and h/H borders are limited by the CAD, or borders are manually fixed: hH_range = [min_hH, max_hH].

  • cartesian_coordinates: list(str, str, str), default = [‘x’, ‘y’, ‘z’]

    Names of the 3 cartesian coordinates.

  • TreatmentPtris: TreatmentPtris<convention>, default = None

    Call an object defined upstream with at least in_vars options.

    For more details, please refer to the corresponding treatment.

Preconditions

The treatment must be applied on a 3D Zone corresponding to a blade skin and its fillet. The Base must have only one Zone and one Instant with reduced height and meridional coordinates (computed with antares.treatment.turbomachine.TreatmenthH).

Postconditions

The output is a mono-zone base containing the variables from the input base, plus the curvilinear curvature coordinate and its reduced form, and the radius. If TreatmentPtris is not None, the input base is also extended with the isentropic Mach number Mis and its reference pressure Ptris.

The input base is a mono-zone base containing the variables defined by the user. It is also extended with the variables:

  • d

    The curvilinear curvature coordinate.

  • d_D

    The reduced form of the previous one.

  • Ptris

    The total isentropic pressure of reference, necessary to compute Mis. Only if a TreatmentPtris<convention> has been called.

  • Mis

    The isentropic Mach number. Only if a TreatmentPtris<convention> has been called.

Examples

import antares

myt = antares.Treatment('UnwrapBlade')
myt['base'] = blade_skin_base
myt['number_of_heights'] = 101
myt['number_of_d_D'] = 1001
base = myt.execute()

If you like to plot a 2D contouring of the unwraped blade on a (d/D, R) plan, the following lines should be added to the previous ones.

from matplotlib.tri import Triangulation

tri = Triangulation(base[0][0]['x'],
                    base[0][0]['y'])
tri.x = base[0][0]['d_D']
tri.y = base[0][0]['R']

If you like the get Mis on the 2D unwraped blade, the following exemple shows an efficient way to do so.

import antares

# Fill Ptris information. For more details,
# refer to the corresponding treatment.
myt_Ptris = antares.Treatment('Ptris'+'convention_name')
myt_Ptris['in_vars'] = ['x', 'y', 'z', 'r', 'CoordinateReducedMeridional',
                        'gamma', 'Cp', 'omega', 'P', 'T']

myt = antares.Treatment('UnwrapBlade')
myt['base'] = blade_skin_base
myt['TreatmentPtris'] = myt_Ptris
base = myt.execute()

Main functions

class antares.treatment.turbomachine.TreatmentUnwrapBlade.TreatmentUnwrapBlade
execute()

Unwrap a 3D blade into a 2D plan.